|
Equilibrium Temperature for exoplanets, possible solutions
|
|
| cirax | Date: Friday, 04.11.2016, 19:33 | Message # 1 |
 Astronaut
Group: Users
 Spain
Spain
Messages: 43
Status: Offline
| There is a problem in SE with temperature for planets if the energy of the main stars doesn't occur mainly in the visual band. Due more than 70% of the stars in our galaxy are red dwarfs (most of their energy occur in the infrared) I find the temperature issue quite important and something that it shouldn't be difficult to fix, just using the Steffan-Boltzmann equation for the equilibrium temperature of a planet (it works in all wavelengths).
Because I did a Proxima b procedural planet, a user called Stefan notice to me that the temperature in the paper for Proxima b was 100ºC out, so I just consulted the wikipedia for equilibrium temperature and applied the equations as it follows:
RADIUS-TEMPERATURE EQUATION
The planetary equilibrium temperature equation for Proxima b is:
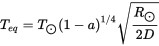
TE=[(TS*(1-a))^(1/4)]*[((RS/(2*D))^(1/2)]
Where:
TE = Equilibrium Temperature for the planet (Kelvin)
TS = Star Temperature (Kelvin)
a = Albedo of the planet
RS = Star Radius (meters)
D = Distance from the star or semimajor axis (meters)
For Proxima b results with the paper data (page 10 data):
TS = 3050 K
a = 0 (ideal black body)
RS = 0.141 RSun = 0.141*696342*1000 = 98184222 meters
D = 0.0485 AU = 0.0485*149600000*1000 = 7255600000 meters
TE = [(3050*(1-0))^(1/4)]*[((98184222/(2*7255600000))^(1/2)] = 250.88 Kelvin = -22.268 Celsius
Quite closer to the 234 K (-39.15 C) of the paper.
For fun I applied the Mars albedo to the upper equation (a=0.25) giving to me 232.85 K or -40.29, almost the value in the paper. But probably I did something wrong because the paper saids clearly 234 K equilibrium temperature for an and ideal black body (a=0). Anyway 250 K is a lot of closer to the real value.
LUMINOSITY EQUATION
Also the derived equation for only known bolometric luminosity is:
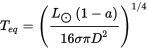
TE = ([(LS)*(1-a)]/[(16*SB*PI*D^2])^(1/4)
Where:
TE = Equilibrium Temperature for the planet (Kelvin)
LS = bolometric luminosity of the star
a = Albedo of the planet
D = Distance from the star or semimajor axis (meters)
SB = Steffan-Boltzmann constant
For Proxima b results with the paper data (page 10 data):
LS = 0.00155 LSun = 0.00155 * 3.846E+26 = 5.96E+23 Watts
a = 0 (ideal black body)
D = 0.0485 AU = 0.0485*149600000*1000 = 7255600000 meters
SB = 5.67E-08
TE = ([(5.96E+23)*(1-0)]/[(16*(5.67E-08)*PI*7255600000^2])^(1/4) = 251.06 K = -22.0896 Celsius, again closer to the 234 K
So both equations (first based in the Radius and Temperature of the star, or the second with just the bolometric luminosity ) seems to be a better solution than the visual magnitude to calculate the temperature of the planets.
The only real problem can be the lack of radius-temperature or bolometric luminosity for the stars, in those cases I think the better solution is using bolumetic magnitude standards depending the spectral classification. I found here, university of rochester, standars for almost all main sequence stars.
For example if I didn't know the bolometric luminosity for Proxima b, I can use the bolometric luminosity value of the standard for an M6V star (Proxima b spectral class) which is 12.3 (figures as Mbol in the standards for M6V document), then I can transform it into bolometric luminosity as it follows:
BOLOMETRIC MAGNITUDE CONVERSION
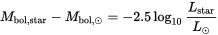
Inverting the upper one:
LS=(10^((MBSun-MBS)/2.5))*LSun
Where:
LS = bolometric luminosity of the star (Times Sun)
MBSun = bolometric luminosity of the Sun = 4.72
MBS = bolometric magnitude of the star = for an M6V Star =12.3
LSun = bolometric luminosity of the Sun (Times Sun) = 1
LS=(10^((4.72-12.3)/2.5))*1 = 0.001037528 (Times Sun) = 3.99E+23 Watts
Applying this to the Temperature of equilibrium with only bolometric luminosity results:
TE = ([(3.99E+23)*(1-0)]/[(16*(5.67E-08)*PI*7255600000^2])^(1/4) = 227.09 K = -46.06 Celsius.
Again a lot of closer to the 234 K for the TE for Proxima b in the paper.
SUGGESTED SOLUTION
So to fix the problem I suggest that when SE reads the catalog and there is:
1 ) Radius and Temperature, uses => TE=[(TS*(1-a))^(1/4)]*[((RS/(2*D))^(1/2)]
2) If theres is only luminosity, then the second one => TE = ([(LS)*(1-a)]/[(16*SB*PI*D^2])^(1/4)
3) None of them, then uses the bolometric magnitude standards, transforms it into bolometric luminosity and uses the second equation.
Notice I did this all just looking and reading the wiki so don't cut my neck if I'm writing stupid things, a hand of a real professional will help us all  , and sorry for my sometimes barbarian english. , and sorry for my sometimes barbarian english.
My work for SE: Click here
Textures for Venus surface in color and the moons of Saturn, Uranus and Neptune.
Catalogs of binary stars, brown dwarfs, black holes and neutron stars.
Proxima b (3 versions).
Edited by cirax - Monday, 07.11.2016, 14:33 |
| |
| |
| SpaceEngineer | Date: Friday, 04.11.2016, 22:01 | Message # 2 |
 Author of Space Engine
Group: Administrators
 Russian Federation
Russian Federation
Messages: 4800
Status: Offline
| SE uses the luminosity equation, but with the bolometric luminosity of the star, not the visual one. The problem may be in the bolometric correction table (a table to convert visual luminosity to bolometric, for each spectral class), it may be imprecise for the very dim stars. Maybe using the radius/temperature equation will give more precise results, but only in the case if radius and temperature are defined in the catalog script. Otherwise SE takes temperature from the table by spectral class, and computes radius from temperature and luminosity (bolometric) using the Stefan–Boltzmann law, so we again obtain the previous result.

|
| |
| |
| cirax | Date: Monday, 07.11.2016, 14:32 | Message # 3 |
 Astronaut
Group: Users
 Spain
Spain
Messages: 43
Status: Offline
| Ok, just using radius and temperature I had a better result for equilibrium temperature.
Anyway when I add data related with luminosity (AppMagn, AbsMagn or Luminosity) the temperature calculation goes far away from the expected. Also surprises me the fact that with only Luminosity (supossed bolometric) gives a result 100º of difference, and both results come from the Steffan-Boltzmann equation. Visual magnitudes are even more strange.
There is an archive with bolometric magnitudes (in the table below link as Mbol) from the most stars in the main sequence, they are mean values of this magnitudes from various known stars of the same spectra, author is Eric Mamajek, University of Rochester, this is the table. Instead using the temperature table (I supposed they are also mean values) you can use this table and with the bolometric magnitude conversion equation, calculate the real bolometric luminosity and finally with second equation the planetary equilibrium temperature. So you don't depend from that bolometric luminosity correction coming from a visual magnitude.
Edit: There is also a column with bolometric luminosity (logL), you maybe want to use it instead converting Mbol.
My work for SE: Click here
Textures for Venus surface in color and the moons of Saturn, Uranus and Neptune.
Catalogs of binary stars, brown dwarfs, black holes and neutron stars.
Proxima b (3 versions).
Edited by cirax - Monday, 07.11.2016, 18:35 |
| |
| |