|
Science and Astronomy Questions
|
|
| Watsisname | Date: Monday, 10.10.2016, 21:01 | Message # 841 |
 Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| quarior14, this seems problematic. If you only know the sidereal rotation rate, and neither the length of solar day nor the orbital period nor the orbital distance, then you have an under-determined system. Basically, how long the solar day will be will depend on how far the planet is from the star, so if you don't know that, then you're stuck. (And orbital distance should be converted to meters when used in Kepler's Third Law).
Do you have any other conditions about the planet to help determine it? Do you know how bright the star is and how warm the planet is, for instance?
|
| |
| |
| quarior14 | Date: Monday, 10.10.2016, 21:09 | Message # 842 |
 World Builder
Group: Users
Pirate
Messages: 649
Status: Offline
| Watsisname, I updated my post, I have the solar period too, but I get a negative orbital period, the planet is retrograde it ?
Quote quarior14 (  ) Watsisname, thanks, but I don't have semimajor axis (it is AU ?), I juste sidereal periods, so I have P sidereal = 1.052165173 years = 313.1561 solar days = 9216.96691325 hours => 1/P sidereal = 1/P solar + 1/P orbital <=> 1/P solar = 1/9216.96691325 - 1/((4π 2a 3)/6.6738480*10 -11*0.8*1.9891*10 30)) Edit : I found this for P orbital :  (Source : Wikipedia) Edit 2 : I'm stupid... 1/P orbital = 1/P sidereal - 1/P solar <=> 1/P orbital = 1/1.052165173 - 1/1.0500000001138413242009132420091 = -0,0019598343188704316143210359517 years P orbital = 1/(-0,0019598343188704316143210359517) = -510,24721343606184076731659026361 years I mistake or it is retrograde ?
Quote Watsisname ( ) Do you have any other conditions about the planet to help determine it? Do you know how bright the star is and how warm the planet is, for instance?
No, I have'nt other informations, juste gravity, solar days, sidereal years and solar years in the book Songs of a Distant Earth.
Quarior
Edited by quarior14 - Monday, 10.10.2016, 23:10 |
| |
| |
| Watsisname | Date: Monday, 10.10.2016, 21:48 | Message # 843 |
|
Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| Hmmm, no, orbital period should not be coming out negative. Let's go through a few examples:
Computing Earth's sidereal day:
The Earth's solar day is 24 hours, and its orbital period is 365 days (not exactly, but close enough). Then to compute Earth's sidereal day,
1/24+1/(24*365))-1 = 23.9344 hours. Which makes sense; the solar day is a bit longer than the sidereal day.
Computing Earth's orbital period:
1/23.9344-1/24)-1 = 8760 hours = 365 days.
Solar period of a retrograde Earth:
Use orbital period of 365 days and sidereal period of 23.9344 hours:
1/23.9344+1/(365*24))-1 = 23.8692 hours. Makes sense; solar day should be shorter than sidereal in this case.
Orbital period of a retrograde Earth:
We started with 365 days. Let's see if we get it back.
1/23.8692-1/23.9344)-1 = 8760 hours = 365 days.
EDIT:
Ugh, the forum is messing up the parentheses, but I think you know what I mean.
Quote quarior14 ( ) No, I have'nt other informations, juste gravity, solar days, sidereal years and solar years in the book Songs of a Distant Earth.
Oh, then what's the problem? You have the orbital period measured in two different ways.  The ratio of the two will tell you the ratio of sidereal day to solar day, as well.
|
| |
| |
| steeljaw354 | Date: Monday, 10.10.2016, 22:58 | Message # 844 |
 World Builder
Group: Users
Pirate
Messages: 862
Status: Offline
| Watsisname, What if Mercury was our moon instead of Theia or the moon we have? Would they lock?
|
| |
| |
| quarior14 | Date: Monday, 10.10.2016, 23:51 | Message # 845 |
|
World Builder
Group: Users
Pirate
Messages: 649
Status: Offline
| Watsisname, so unit it is hours.
1/Porbital = 1/Psidereal - 1/Psolar
Quote Watsisname ( ) Earth's sidereal day, 1/24+1/(24*365)-1 = 23.9344 hours. Which makes sense; the solar day is a bit longer than the sidereal day.
If I apply for Thalassa, Thalassa's sidereal day : (1/29.4325)+(1/(29.4325*x))-1 = (1/29.4325)*(1+(1/x))
x it is the orbital period but I don't know. I can put the solar year or sidereal year in place ?
Quote Watsisname ( ) Oh, then what's the problem? You have the orbital period measured in two different ways. The ratio of the two will tell you the ratio of sidereal day to solar day, as well.
Not really understand, if I recup :
Dsidereal = (1/Dsolar) + (1/Ysolar)-1
Porbital = Yorbital = (1/Dsidereal) - (1/Dsolar)-1
It is correct ?
I just redo your calculation for the Earth, I do not find at all the same thing
Dsidereal = (1/24) + (1/(24*365))-1 = (1/24) + (1/(24*365)-1) = 8760.041667 =/= 23.9344 hours
And if I did Dsidereal = (1/24) + (1/(24*(365)-1)) = 15.25 =/= 23.9344 hours
By cons it's okay if I did Dsidereal = ((1/24) + (1/(24*365)))-1 = 23.9344 hours
I deduce that :
Dsidereal = ((1/Dsolar) + (1/Ysolar))-1
Porbital = Yorbital = ((1/Dsidereal) - (1/Dsolar))-1
For Thalassa :
Dsidereal = ((1/29.4325) + (1/(29.4325*312.5116793))-1 = 29.33861992 hours
Porbital = Yorbital = ((1/29.33861992) - (1/29.432))-1 = 9198.000001 hours = 312.5116793 solar days = 383.25 Earth's solar days = 1.05 Earth's solar years
It is correct ?
And the sidereal day it is the rotation period ?
Quarior
Edited by quarior14 - Monday, 10.10.2016, 23:56 |
| |
| |
| Watsisname | Date: Tuesday, 11.10.2016, 00:05 | Message # 846 |
|
Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| steeljaw:
Short answer: definitely.
It is pretty hard to not have a planet and moon become tidally locked over millions to billion year timescales. They have the be very widely separated. (Recall that 6th power dependence on the orbital distance). This is why most close to intermediate-range moons in the solar system are locked.
Slightly longer answer:
An easy way to compare numbers for tidal locking time -- if you already have one computed for another body, as we have done -- is as follows: The locking time is proportional to the density of the satellite, its initial spin rate, and the sixth power of its orbital distance. It is inversely proportional to the square of the mass of the primary body. The 6th power of orbital distance tends to be the most important factor. y=x6 grows very fast. But in this case if we just replace Theia with Mercury (about half the mass, a bit more dense, and a bit smaller), then the result doesn't change very much -- not by more than an order of magnitude. So it still gets locked in about the same timescale -- millions of years.
quarior14, sorry, I have to run -- let me get back to you later with a complete answer. For now, the unit you use is whatever you want it to be, as long as you are consistent. Hours is convenient sometimes.
|
| |
| |
| quarior14 | Date: Tuesday, 11.10.2016, 08:47 | Message # 847 |
|
World Builder
Group: Users
Pirate
Messages: 649
Status: Offline
| Quote Watsisname ( ) quarior14, sorry, I have to run -- let me get back to you later with a complete answer. For now, the unit you use is whatever you want it to be, as long as you are consistent. Hours is convenient sometimes.
OK, and it's true that hours are practices. Do not complicated with the hours, it's the same here : 1 hour = 3600 seconds
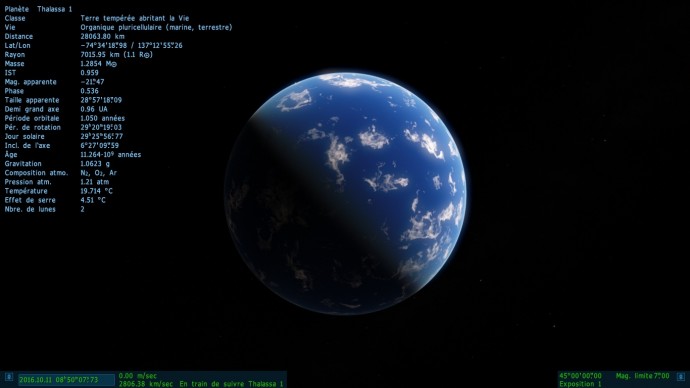
Looks like it's okay, in Space Engine, I get for solar day 29h25m56.77s.
I convert my solar day : 29.4325 h = 29 h 25.95 m = 29 h 25 m 57 s, it just a shift of 57-56.77 = 0.23 s, perhaps due to rounding for the period. Thank you for your formula !
Quarior
Edited by quarior14 - Tuesday, 11.10.2016, 08:56 |
| |
| |
| steeljaw354 | Date: Tuesday, 11.10.2016, 10:31 | Message # 848 |
|
World Builder
Group: Users
Pirate
Messages: 862
Status: Offline
| Watsisname, I understand now.
|
| |
| |
| DoctorOfSpace | Date: Tuesday, 11.10.2016, 20:30 | Message # 849 |
 Galaxy Architect
Group: Global Moderators
Pirate
Messages: 3600
Status: Offline
| I think this is more directed towards Watsisname, but I welcome others input.
While watching a rendering of a warp bubble the antigravity region of the bubble appeared to become disconnected from the rest and move on its own.
This made me wonder what one would perceive of an object moving at superluminal velocities.
How would an object appear to someone if it exceeded the speed of light?
Does the object simply vanish once it exceeds c, does one see it run in the reverse direction, or would something else happen entirely?
This is assuming it had a way to reach c and exceed it and assuming you could actually see the object.
Intel Core i7-5820K 4.2GHz 6-Core Processor
G.Skill Ripjaws V Series 32GB (4 x 8GB) DDR4-2400 Memory
EVGA GTX 980 Ti SC 6GB
|
| |
| |
| Destructor1701 | Date: Tuesday, 11.10.2016, 21:01 | Message # 850 |
|
Pioneer
Group: Users
Ireland
Messages: 533
Status: Offline
| As I understand it, the first photons emitted by the ship that could possibly reach you would be the ones emitted as the ship passed its nearest flyby range to you.
So it would appear to pop into existence at that location.
Then, the next photons to reach your eyes would be from the moment both before and after the ship passed closest approach.
So it would split into two images as soon as it appeared, and both would recede at what appeared to be FTL velocities from one another. The forward version may appear to recede faster, not sure.
As to the gravitational lensing distortion and doppler colour/wavelength distortions, I couldn't begin to guess.
|
| |
| |
| Watsisname | Date: Thursday, 13.10.2016, 07:45 | Message # 851 |
|
Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| Destructor has it right. The object would appear to suddenly pop into existence and split in two -- one moving backwards and the other moving forwards.
Which one appears to move faster? Let's work it out.
Consider a particle moving in a straight line at twice the velocity of light. The particle passes by an observer (at rest) with a closest approach of one light second distance.
Let t=0 be the time (in the rest frame) that the particle was at its minimum distance. Then at t=1s, it has moved a distance of 2 light seconds further along. And at t=-1s, it was 2 light seconds back.
When does the observer receive the light from these three moments (t=-1, 0, and 1)?
From the particle at t=0 to the observer it is a distance of 1 light second, so the light arrives at t=1s.
By Pythagorean theorem, the distance from the particle at t=1 to the observer is sqrt(12 + 22) = sqrt(5) ~2.24 light seconds. By symmetry, the distance from the observer to the particle at t=-1s is the same.
The light from the particle at t=-1 reaches the observer at -1+2.24 = 1.24s
The light from the particle at t=1 reaches the observer at 1+2.24 = 3.24s
Therefore the observer sees it take 2.24 seconds for the particle "moving forward" to progress one light second of distance, while it only takes 0.24 seconds for the particle "moving backwards" to progress the same distance. This one seems faster than light.
Pretty weird!
Added: In fact, this very mechanism of the particle seeming to move faster than light on its approach part holds true even for particles moving slower than light. We see the effect with relativistic jets from active galactic nuclei, pointed in our direction. For example, the jet of M87. (See bottom of page.)
|
| |
| |
| PlutonianEmpire | Date: Friday, 14.10.2016, 06:30 | Message # 852 |
 Pioneer
Group: Users
United States
Messages: 475
Status: Offline
| I was working on one of my own custom planets, when I was wondering about the breathability of my atmosphere for that world.
My composition for a surface pressure of 1.62 atm: 0.976 atm N2 (60.2 % ) , 0.459 atm O2 (28.3 % ) , 0.112 atm H2O (6.92 % ) , 0.0745 atm Ar (4.59 % ) , 221 ppm CO2, 3.8 ppm SO2, 1.68 ppm H2S. Obviously my question involves the final two gases. I tried to follow the table in the Breathable Atmosphere thread, but didn't want to kill humans trying to live there. I do know that SO2 and H2S are stinky gases.
So is this planet livable? And what exactly might the air smell like there?
Specs: Dell Inspiron 5547 (Laptop); 8 gigabytes of RAM; Processor: Intel® Core™ i5-4210U CPU @ 1.70GHz (4 CPUs), ~2.4GHz; Operating System: Windows 7 Home Premium 64-bit; Graphics: Intel® HD Graphics 4400 (That's all there is :( )
Edited by PlutonianEmpire - Friday, 14.10.2016, 06:35 |
| |
| |
| Watsisname | Date: Friday, 14.10.2016, 10:31 | Message # 853 |
|
Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| It would smell like burnt matches and rotten eggs (the sulfur dioxide and hydrogen sulfide gases, respectively -- both are above the odor threshold). The air be safe to breathe for a while, but it would cause some respiratory problems.
It is hard to say if it would be permanently habitable. The problem is you have 1.62atm of pressure, so this is actually equivalent to 6.2ppm of SO2 at Earth's pressure. This is above the OSHA permissible exposure limit for an 8 hour work period (5ppm), but well below the "immediately dangerous to life and health" level of 100ppm.
The H2S concentration is equivalent to 2.72ppm at Earth's pressure. This isn't dangerous, but it would be unpleasant, both by the odor and its effect on your health (it irritates the eyes, causes headaches, loss of sleep, and overall just isn't very fun.)
Of the two, I think the SO2 would be the less pleasant at those concentrations.
|
| |
| |
| Huesudo | Date: Friday, 14.10.2016, 13:27 | Message # 854 |
|
Observer
Group: Users
Spain
Messages: 11
Status: Offline
| Quote Watsisname ( ) Of the two, I think the SO2 would be the less pleasant at those concentrations.
I don't know. I love the smell of burnt matches 
|
| |
| |
| Watsisname | Date: Friday, 14.10.2016, 15:43 | Message # 855 |
|
Galaxy Architect
Group: Global Moderators
United States
Messages: 2613
Status: Offline
| At several ppm concentration, continuously? I guarantee you don't  SO2 gas becomes sulfuric acid on contact with water. That includes in your eyes and mucous membranes.
|
| |
| |
ENG
New site
United States 
Pirate 
Ireland 
Spain